Microfacet Theory

Sep 9 2018 Rendering 7 minutes read (About 1001 words)

微面元理论

微面元理论认为粗糙表面是由细小的微面组成的,每个微面元都满足完美镜面反射

$$\omega_h = \omega_i \hat{+} \omega_o$$

$$d\Phi_h = L_i(\omega_i)d\omega_i dA^{\perp}(\omega_h) = L_i(\omega_i)d\omega_i cos\theta_h dA(\omega_h)$$

$$dA(\omega_h) = D(\omega_h)d\omega_h dA$$

$D(\omega_h)$:法线分布项,描述微面元的法线为$\omega_h$的比例,只有法线为$\omega_h$的才能被看见

$$\Rightarrow d\Phi_h = L_i(\omega_i)d\omega_i cos\theta_h D(\omega_h)d\omega_h dA$$

假设每个微面元都各自按照Fresnel's Law反射光线

$$\Rightarrow d\Phi_o = F_r(\omega_o)d\Phi_h$$

$$\because L(\omega_o) = \frac{d\Phi_o}{d\omega_o cos\theta_o dA}$$

$$\therefore L(\omega_o) = \frac{F_r(\omega_o)L_i(\omega_i)d\omega_i cos\theta_h D(\omega_h) d\omega_h dA}{d\omega_o cos\theta_o dA}\tag{1}$$

接下来计算$\frac{d\omega_h}{d\omega_i}$,考虑基于$\omega_o$的球坐标系,如下图: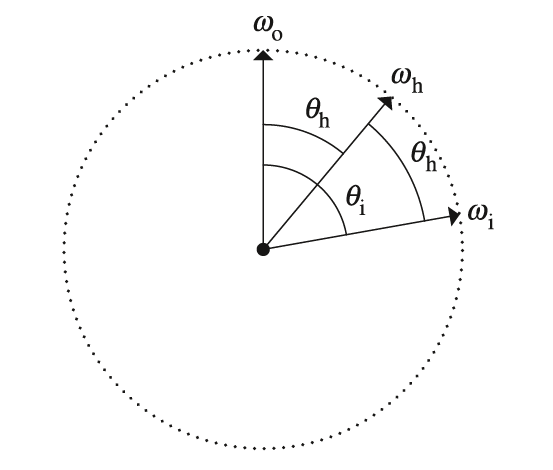
$基于$\omega_o$的球坐标系,来源PBRT$

$$\frac{d\omega_h}{d\omega_i} = \frac{sin\theta_h d\theta_h d\phi_h}{sin\theta_i d\theta_i d\phi_i}$$

$$\because \theta_i = 2\theta_h$$

$$\therefore \frac{d\omega_h}{d\omega_i} = \frac{sin\theta_h d\theta_h d\phi_h}{sin(2\theta_h)2d\theta_h d\phi_h} = \frac{sin\theta_h}{4sin\theta_h cos\theta_h} = \frac{1}{4cos\theta_h}$$

$$\Rightarrow \frac{d\omega_h}{d\omega_i} = \frac{1}{4cos\theta_h} = \frac{1}{4\omega_i \cdot \omega_h} = \frac{1}{4\omega_o \cdot \omega_h}$$
$$\Rightarrow \frac{d\omega_h}{d\omega_o} = \frac{1}{4cos\theta_h} = \frac{1}{4\omega_i \cdot \omega_h} = \frac{1}{4\omega_o \cdot \omega_h}$$

代入(1)式:
$$\Rightarrow L(\omega_o) = \frac{F_r(\omega_o)L_i(\omega_i)D(\omega_h)d\omega_i}{4cos\theta_o}$$

$$\because L(\omega_o) = L(\omega_i) f_r(p,\omega_i, \omega_o)cos\theta_i d\omega_i$$

$$\therefore f_r(p,\omega_i,\omega_o) = \frac{L(\omega_o)}{L(\omega_i) cos\theta_i d\omega_i} = \frac{F_r(\omega_o)D(\omega_h)}{4cos\theta_i cos\theta_o} = \frac{F_r(\omega_o)D(\omega_h)}{4(n\cdot l)(n \cdot v)}$$

再乘上一个几何衰减项G,用于描述微面元被遮挡或者处于阴影中的比例

$$\Rightarrow f_r(p,\omega_i,\omega_o) = \frac{F_r(\omega_o)D(\omega_h)G(\omega_i,\omega_o)}{4cos\theta_o cos\theta_i}$$

接下来讲下D,F,G的常用实现方案

法线分布项

GGX

$$D(h) = \frac{\alpha^2}{\pi((n\cdot h)^2(\alpha^2 - 1) + 1)^2}$$
$$\alpha = roughness^2$$

roughness: 粗糙度

float D(float alpha, float NdotH)
{
    float alphaSqr = sqr(alpha);
    float denominator = sqr(NdotH) * (alphaSqr - 1.0f) + 1.0f;
    float D = alphaSqr / (PI * sqr(denominator));
    return D;
}

几何衰减项

Smith

Smith函数对G做了一个近似,即假设入射遮挡与出射遮挡是不相关的,因此可以被分离开来

$$G(l,v,h) = G_1(n,l)G_1(n,v)$$
$$G_1(n,v) = \frac{n\cdot v}{(n\cdot v)(1 - k) + k}$$
$$k = \frac{(Roughness + 1)^2}{8}$$

实现:

float K(float _Roughness)
{
    float modifiedRoughness = _Roughness + 1;
    return sqr(modifiedRoughness) / 8;
}

float G1(float k, float NdotV)
{
    return NdotV / (NdotV * (1 - k) + k);
}

float G_Smith(float _Roughness, float NdotL, float NdotV)
{
    float k   = K(_Roughness);
    float G1L = G1(k, NdotL);
    float G1V = G1(k, NdotV);
    float G = G1L * G1V;
    return G;
}

菲涅尔项

Shclick

原始的菲涅尔公式计算比较复杂,一般都是使用如下方程进行近似:

$$F_{schlick}(F_0,l,h) = F_0 + (1 - F_0)(1-(l\cdot h))^5$$

$F_0$: 入射光垂直于表面时的菲涅尔反射率值,也称之为镜面颜色

$$F(0) = (\frac{\eta_i - \eta_o}{\eta_i + \eta_o})^2$$

以下为常见材质的F(0)值

Material	F(0) (Linear)	F(0) (sRGB)
Water	0.02,0.02,0.02	0.15,0.15,0.15
Plastic / Glass (Low)	0.03,0.03,0.03	0.21,0.21,0.21
Plastic High	0.05,0.05,0.05	0.24,0.24,0.24
Glass (High) / Ruby	0.08,0.08,0.08	0.31,0.31,0.31
Diamond	0.17,0.17,0.17	0.45,0.45,0.45
Iron	0.56,0.57,0.58	0.77,0.78,0.78
Copper	0.95,0.64,0.54	0.98,0.82,0.76
Gold	1.00,0.71,0.29	1.00,0.86,0.57
Aluminum	0.91,0.92,0.92	0.96,0.96,0.97
Silver	0.95,0.93,0.88	0.98,0.97,0.95

代码实现:

float SchlickFresnel(float4 SpecColor, float lightDir, float3 halfVector)
{
    return SpecColor + (1 - SpecColor) * pow(1 - dot(lightDir, halfVector), 5);
}

Reference

Physically-Based Shading Models inFilm and Game Production

#Rendering