Jun 2 2025 32 minutes read (About 4783 words)

Shadow

基本实现

通过从灯光视角渲染场景生成深度图(ShadowMap)，渲染主视角的像素时将其变换到灯光空间与灯光空间的深度进行比较

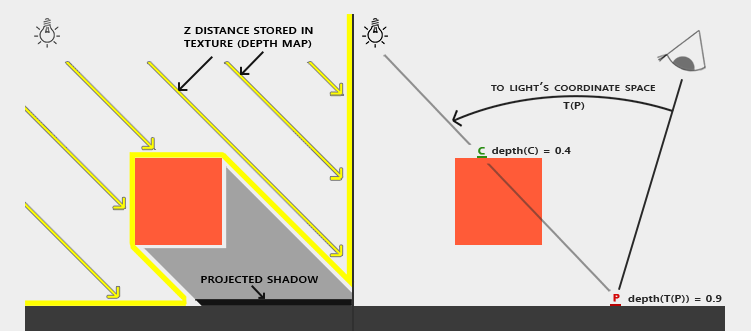
ShadowMap

常规的比较是ShadowMap深度比像素深度(灯光空间)更近，则认为像素被遮挡位于阴影中。

UE中为了减少自遮挡引入了深度过渡区间，当像素深度更远且ShadowMap的深度差大于该过渡值才完全位于阴影中

// Using a soft transition based on depth difference
// Offsets shadows a bit but reduces self shadowing artifacts considerably
float TransitionScale = Settings.TransitionScale;

// ShadowFactor=0 if ShadowMapDepth <= (SceneDepth - 1/TransitionScale)
float ShadowFactor = saturate((ShadowMapDepth - SceneDepth) * TransitionScale + 1);

Bias

由于ShadowMap的分辨率有限，ShadowMap的每个像素必然对应于场景的一片区域

如下图中光线代表像素中心，黑色的区域在灯光空间都被判定为大于像素中心的深度，即处于阴影中

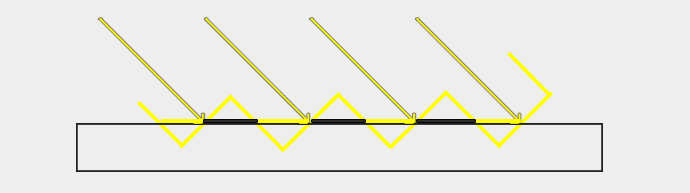
Shadow Map Texel Mapping Area Shadow Acne

通过给定一个Depth Bias可以解决该问题，但同时也引入了另一个问题：Peter Panning（即阴影的位置发生了偏移）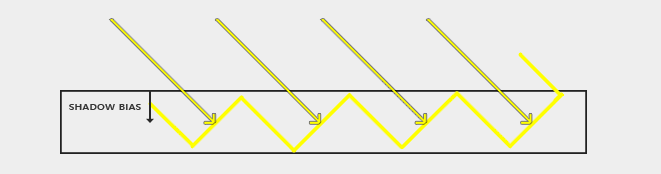
ShadowBias

Depth Bias通常使用常量偏移，但太小容易发生自遮挡，太大对于薄的表面容易出现漏光

Depth Bias

继续以平面为例，$|AB|$为近平面上的一个像素区域，$E$点为像素中心，渲染ShadowMap时记录的是F点的深度

$|FD|$段都将被判定为在阴影中，需将$D$点的深度偏移至$G$才能不发生自遮挡，偏移距离为：
$$
\begin{equation}
\begin{aligned}
DepthBias(D) &= |FG|\cdot tan(\theta)\
&=\frac{|AB|}{2}\cdot tan(\theta)\
&=\frac{FrustumSize}{ShadowMapSize \times 2}\cdot tan(\theta)
\end{aligned}
\end{equation}
$$
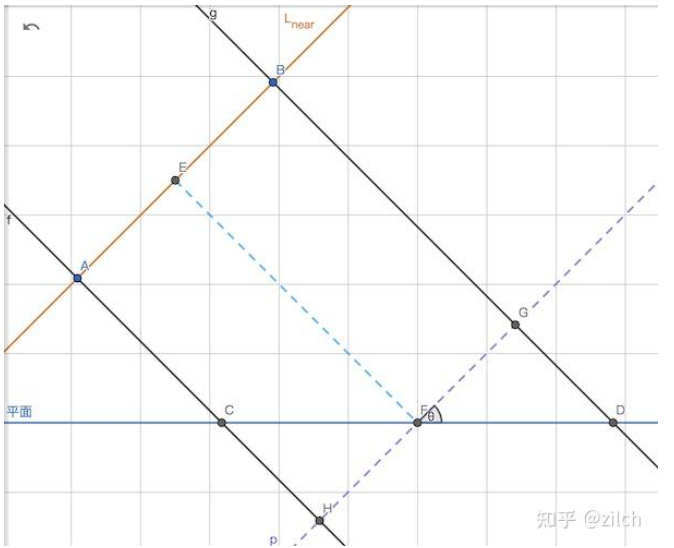
Shadow Bias Math Model

当光方向与平面几乎平行时，单个像素对应的范围将会非常大，以上述公式为例，$\theta$将趋紧于90，$tan(\theta)$为无限大

Slope Scale Depth Bias

通常为了简化$tan$或$sin$的计算，会改用Slope Scale的方式：

1	DepthBias = SlopeDepthBias * Slope + ConstantDepthBias

Slope：与当前Pixel所在三角形的斜率有关，值越大表示越倾斜
SlopeDepthBias：自定义系数
ConstantDepthBias：基础偏移值

Slope通常使用以下公式计算：

1	float Slope = clamp(abs(NoL) > 0 ? (1.0 - NoL) : MaxSlopeDepthBias, 0, MaxSlopeDepthBias);

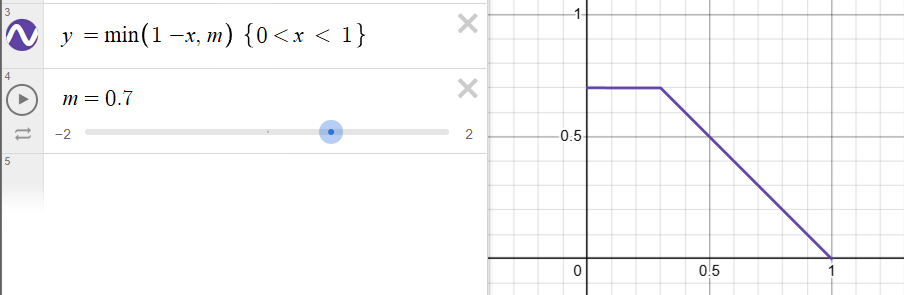
Basic Slope

UE中使用

1	const float Slope = clamp(abs(NoL) > 0 ? sqrt(saturate(1 - NoL*NoL)) / NoL : MaxSlopeDepthBias, 0, MaxSlopeDepthBias);

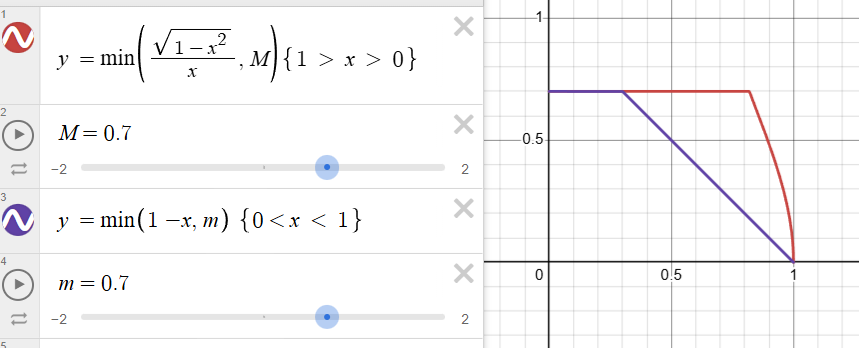
UE Slope

Normal Bias

由于Depth Bias存在光方向与平面平行时失效的问题，我们可以改用向Normal方向偏移：

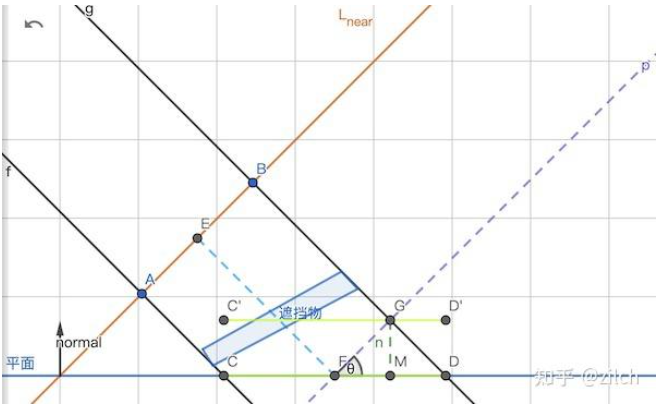
Normal Bias Math Model

Bias的长度为$|GM|$，偏移后$C \rightarrow C^{\prime}$，$D \rightarrow D^{\prime} $，根据计算公式可知不会出现无穷大失效的情况：
$$
|GM| = |FG|\cdot sin(\theta) = \frac{|AB|}{2}\cdot sin(\theta) = \frac{FrustumSize}{ShadowMapSize \cdot 2}\cdot sin(\theta)
$$

在$|AB|$与平面之间不存在遮挡物时，$|C^{\prime}G|$在当前像素不会出现自遮挡的情况，$|GD^{\prime}|$会出现在临近像素区域也不会被遮挡

但当出现上图中的遮挡物时，将导致$C$点漏光。且若临近像素的$|DD^{\prime}|$区间出现遮挡物时，$D$点也将漏光，出现两端漏光的情况

Caster Bias & Receiver Bias

前面我们都是默认Receiver Bias，即PS阶段进行Depth Bias再与ShadowMap记录的深度值进行比较

Caster Bias是在ShadowMap生成的VS阶段对遮蔽物进行反向偏移，其优劣如下：

优点：
- 基于顶点计算，开销低
缺点：
- 仅考虑顶点法线，未考虑像素级的Normal(如应用NormalMap)，精度不足

PCF

由于像素深度与ShadowMap值比较的结果是个二值函数，在阴影边缘会呈现出锯齿状

为解决该问题，引入了Percentage Closer Filter(PCF)：
$$
PCF(x_0, y_0) = \frac{1}{W}\sum_{(x_i, y_i)\in N}\omega(x_i, y_i)\cdot f(x_i, y_i)\
f(x, y) =
\begin{cases}
1, \quad if z_{receiver} <= z_{shadow}(x, y)\quad (光照)\
0, \quad otherwise\quad(阴影)
\end{cases}
$$

$x_0, y_0$：像素投影到ShadowMap的UV

PCF本质是对邻域的深度比较结果进行滤波，UE中使用的分离卷积核，每个像素的权重为U，V权重的乘积：

5x5的权重分布为：

1 2	U: 1-dx, 1, 1, 1, 1, dx V: 1, 1-dy, 1, 1, dy, 1

3x3的权重分布为：

1 2	U: 1-dx, 1, 1, dx V: 1, 1-dy, dy, 1

2x2的权重分布：

1 2	U: 1-dx, 1, dx V: 1-dy, 1, dy

1x1的权重分布：

1 2	U: 1-dx, dx V: 1-dy, dy

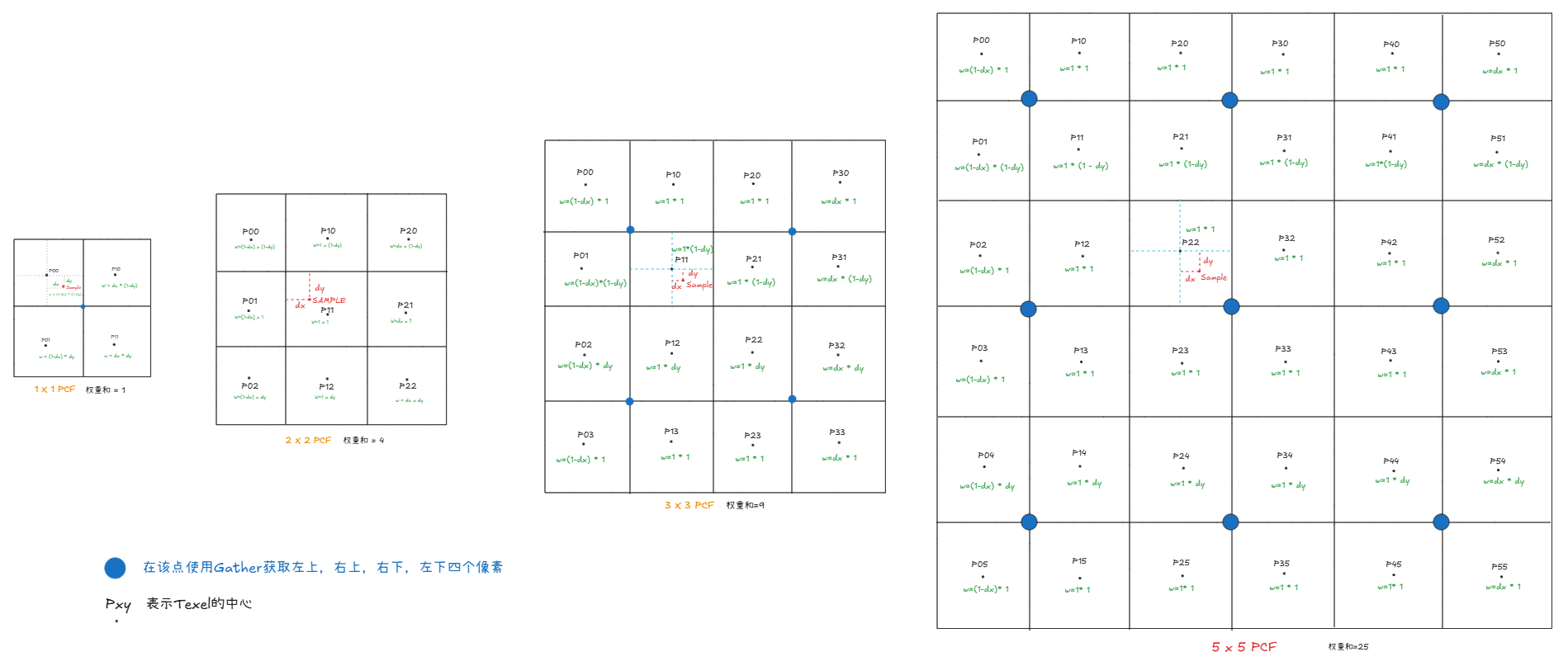
PCF And Weight

Gather获取四个像素时按照(-,+)，(+,+)，(+,-)，(-,-)的原则：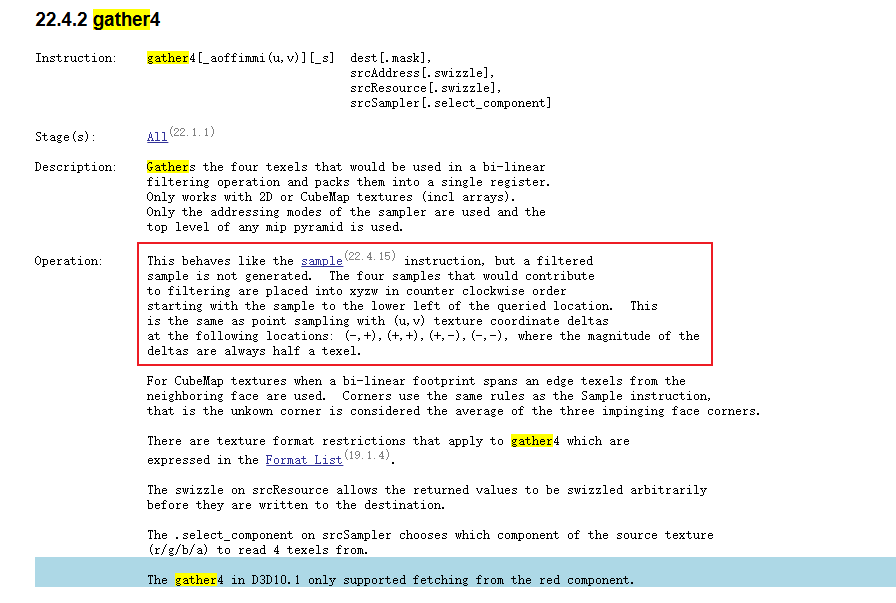
D3D Gather Rule

连续Tent Filter

前面以Texel中心代替Texel，每个Texel根据分布分配一个离散权重。

连续Tent Filter也是分离卷积的方案，根据各Texel的积分结果计算权重并归一化

PCF5x5为例，以采样点Texel中心为坐标原点，单方向的卷积核定义为：$max(2.5 - |x - dx|, 0)$，则任意点的值为：
$$
f_w(u,v) = \max(2.5-|u - dx|, 0)\cdot \max(2.5 -|v - dy|, 0)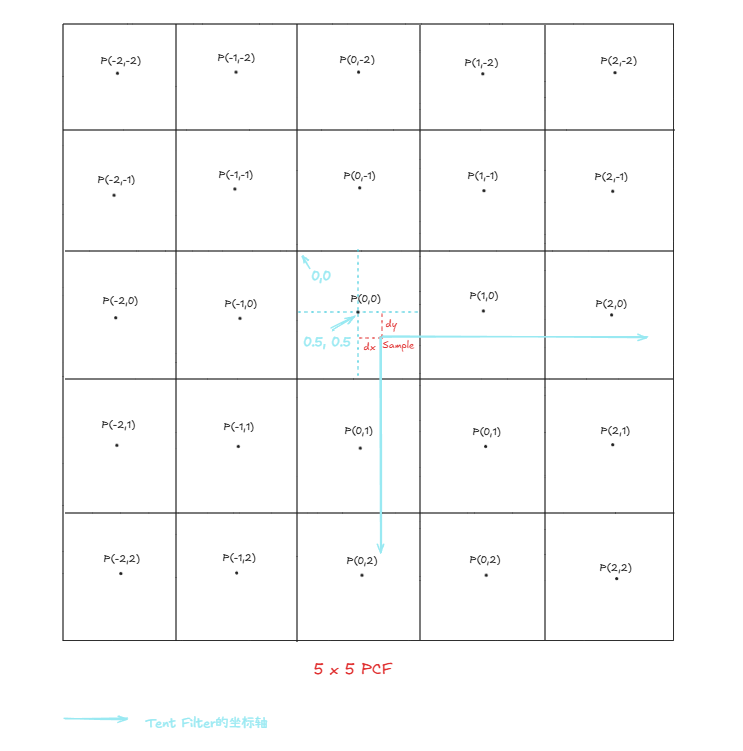
$$
Tent Filter Coordinate

计算像素$i,j$所占的体积：
$$
A_{i,j} = \int_{i - 0.5}^{i + 0.5}\int_{j - 0.5}^{j + 0.5}max(2.5-|u-dx|, 0)\cdot max(2.5-|v-dy|, 0)dudv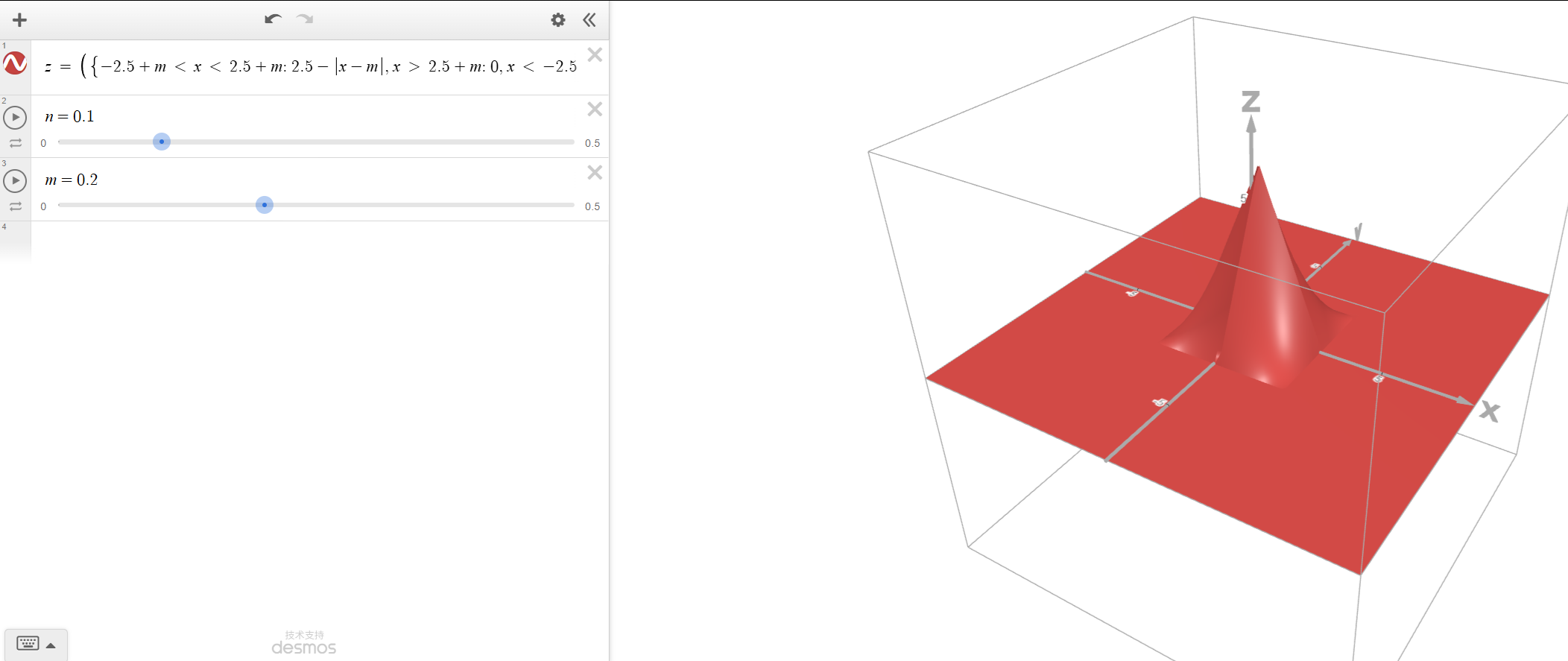
$$

连续Tent Filter

归一化系数：
$$
\begin{equation}
\begin{aligned}
W &= \int_{u = -2.5+dx}^{2.5+dx}\int_{v = -2.5+dy}^{2.5+dy}max(2.5-|u-dx|, 0)\cdot max(2.5-|v-dy|, 0)dudv\
&= \int_{u = -2.5+dx}^{2.5+dx}max(2.5-|u-dx|, 0)du \cdot \int_{v = -2.5+dy}^{2.5+dy} max(2.5-|v-dy|, 0)dv\
&= \int_{u^{\prime} = -2.5}^{2.5}max(2.5-|u^{\prime}|, 0)du^{\prime} \cdot \int_{v^{\prime} = -2.5}^{2.5} max(2.5-|v^{\prime}|, 0)dv^{\prime}\
&=\frac{5\times 2.5}{2}\cdot \frac{5\times 2.5}{2}\
&=\frac{625}{16}\
&=39.0625
\end{aligned}
\end{equation}
$$

PCSS

CSM

将视椎体划分为多个子视椎体，每个子视椎体对应的ShadowMap尺寸一致，以实现各级不同的精度控制

子视椎体划分通常按照指数分布，以三级Cascade为例，假设分布指数为$\alpha$，则各级的分布比例为：$1, \alpha, \alpha^2$

CSM Distribution

投影半径

本质是求解子视椎体的最小包围球，如下图所示即求：$min(a^2+c^2, d^2+b^2)$

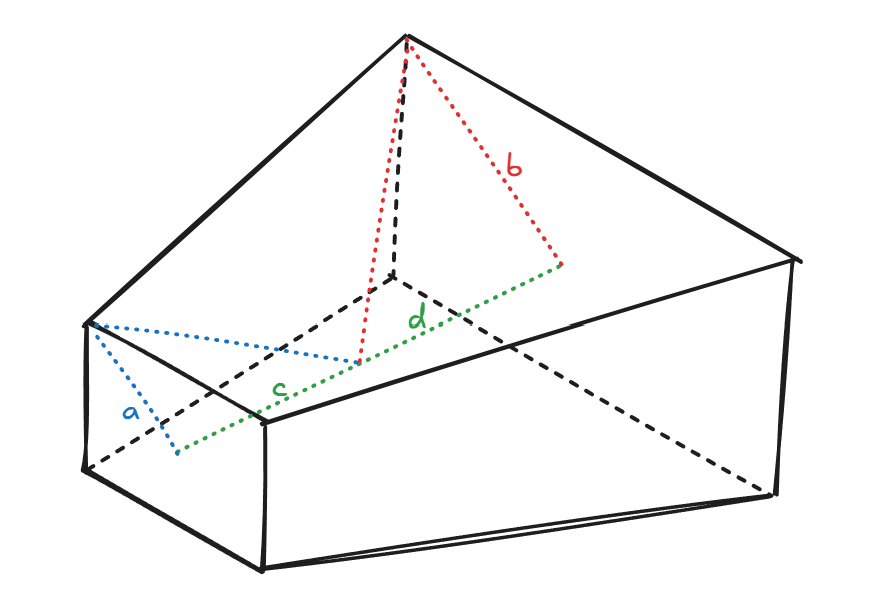
CSM Radius

对于指定CSM级别而言$c+d$是确定值，$a$与$b$也是固定值(为其所属截面的对角线)

令：$d = l - c$，则求解$c$满足$min(a^2+c^2, b^2+(l-c)^2)$，且$b^2 > a^2$。其图像如下图所示，最小值在二者的交点处取到：
$$
\begin{equation}
\begin{aligned}
a^2+c^2 &= b^2+(l-c)^2\
a^2+c^2 &= b^2+l^2+c^2-2\cdot l \cdot c\
2\cdot l \cdot c &= b^2+l^2-a^2\
c &= \frac{b^2+l^2-a^2}{2\cdot l}
\end{aligned}
\end{equation}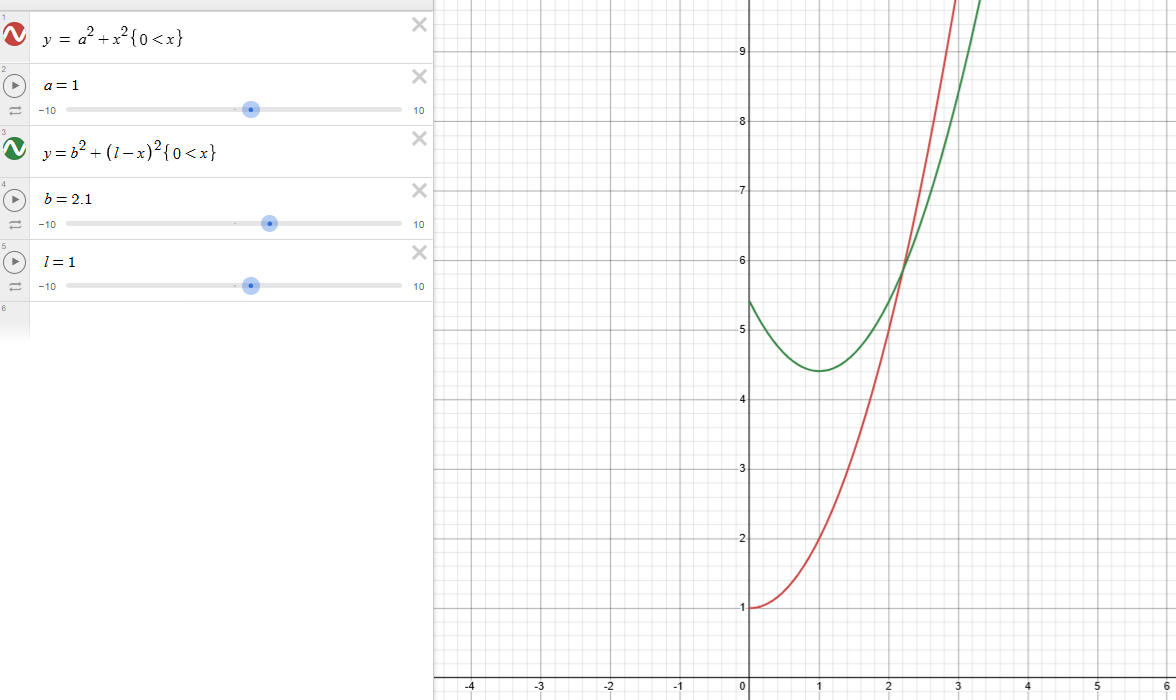
$$
CSM Radius Visualize

Bias

由于CSM是每级分辨率一致但对应的视椎体范围不一致，因此各级Cascade应用的Bias也不一样

隔帧更新

控制不同级别Cascade的更新频率，远处的信息变化慢，可以隔N帧更新一次

原神的分享中提到使用了八级CSM，采用前四级每帧更新，后四级每帧轮流更新的策略

由于CSM的生成是基于子视椎体，当视角变化时，WorldToLight矩阵也在随之发生变化。

因此要实现缓存策略，必须记录下CSM生成时的WorldToLight矩阵，将当前帧像素从World Space变化到N帧前的LightSpace采样CSM

1
2
3

float3 LightSpacePos = CurWorldPosition * PrevWorldToLight;
float CSMDepth = CSM.Sample(Sampler, LightSpacePos.xy);
bool inShadow = LightSpacePos > CSMDepth; // 假设深度越小越近

Scrolling

对于近处的CSM而言，复用历史帧的ShadowDepth时，需要在Receiver阶段使用Bias？？？

Variance Shadow Map

RSM

ShadowVolume

PlaneShadow

公式推导

以下推导基于世界空间坐标

平面方程定义：$$\vec{N}$$为平面法线，$$\vec{Q}$$为平面上一点，d为原点到该平面最短距离的负值
$$
$$\begin{equation} \vec{N} \cdot \vec{Q} + d = 0 \end{equation}
$$

假设，模型点位于$$\vec{P}$$，方向光方向为$$\vec{L}$$，其投影到平面上的位置为$$\vec{Q}$$，则：
$$
\begin{equation} \vec{Q} = \vec{P} + t * \vec{L} \end{equation}
$$

因此，可以求解t：

$$
\begin{equation}
\begin{aligned}
\vec{N} \cdot (\vec{P} + t * \vec{L}) + d = 0 \
t = -\frac{d + \vec{N} \cdot \vec{P}}{\vec{N} \cdot \vec{L}}
\end{aligned}
\end{equation}
$$
此时将$t$代入(2)中，即可求解$$\vec{Q}$$

$$
\begin{equation}
\vec{Q} = \vec{P} - \frac{d + \vec{N} \cdot \vec{P}}{\vec{N} \cdot \vec{L}} * \vec{L}
\end{equation}
$$

然而，我们期望的是计算出一个投影矩阵$$\vec{M}$$，能够得到$$\vec{Q} = \vec{M} \cdot \vec{P}$$，接下来我们开始构造，首先两边乘以$$\vec{N} \cdot \vec{L}$$:

$$
\begin{equation} (\vec{N} \cdot \vec{L}) \vec{Q} = (\vec{N} \cdot \vec{L}) \vec{P} - d \vec{L} - (\vec{N} \cdot \vec{P}) \vec{L} \end{equation}
$$

首先将$$(\vec{N} \cdot \vec{P})* \vec{L}$$分解为向量形式：

$$
\begin{equation} \begin{bmatrix} (N_x P_x + N_y P_y + N_z P_z) L_x \ (N_x P_x + N_y P_y + N_z P_z) L_y \ (N_x P_x + N_y P_y + N_z P_z) L_z \ \end{bmatrix} = \begin{bmatrix} N_x L_x & N_y L_x & N_z L_x \ N_x L_y & N_y L_y & N_z L_y \ N_x L_z & N_y L_z & N_z * L_z \ \end{bmatrix} \cdot \begin{bmatrix} P_x \ P_y \ P_z \ \end{bmatrix} \end{equation}
$$

展开为向量形式：

$$
\begin{equation} (\vec{N} \cdot \vec{L}) \begin{bmatrix} Q_x \ Q_y \ Q_z \ \end{bmatrix} = (\vec{N} \cdot \vec{L}) \begin{bmatrix} P_x \ P_y \ P_z \ \end{bmatrix} - \begin{bmatrix} d L_x \ d L_y \ d L_z \ \end{bmatrix} - \begin{bmatrix} N_x L_x & N_y L_x & N_z L_x \ N_x L_y & N_y L_y & N_z L_y \ N_x L_z & N_y L_z & N_z L_z \ \end{bmatrix} \cdot \begin{bmatrix} P_x \ P_y \ P_z \ \end{bmatrix} \end{equation}
$$

两边除以$$\vec{N} \cdot \vec{L}$$并整理可得：

$$
\begin{equation} \begin{bmatrix} Q_x \ Q_y \ Q_z \ \end{bmatrix} = \begin{bmatrix} 1 - \frac{N_x L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_x}{\vec{N} \cdot \vec{L}} \ -\frac{N_x L_y}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_y L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_y}{\vec{N} \cdot \vec{L}} \ -\frac{N_x L_z}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_z}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_z L_z}{\vec{N} \cdot \vec{L}} \ \end{bmatrix} \cdot \begin{bmatrix} P_x \ P_y \ P_z \ \end{bmatrix} - \frac{1}{ \vec{N} \cdot \vec{L}} \begin{bmatrix} d L_x \ d L_y \ d * L_z \ \end{bmatrix} \end{equation}
$$

对于最后的平移项，可以通过将矩阵变为4x4进而整合到一起

$$
\begin{equation} \begin{bmatrix} Q_x \ Q_y \ Q_z \ 1 \ \end{bmatrix} = \begin{bmatrix} 1 - \frac{N_x L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_x}{\vec{N} \cdot \vec{L}} & -\frac{d L_x}{\vec{N} \cdot {\vec{L}}} \ -\frac{N_x L_y}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_y L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_y}{\vec{N} \cdot \vec{L}} & -\frac{d L_y}{\vec{N} \cdot {\vec{L}}}\ -\frac{N_x L_z}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_z}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_z L_z}{\vec{N} \cdot \vec{L}} & -\frac{d L_z}{\vec{N} \cdot {\vec{L}}}\ 0 & 0 & 0 & 1 \ \end{bmatrix} \cdot \begin{bmatrix} P_x \ P_y \ P_z \ 1 \ \end{bmatrix} \end{equation}
$$

因此，最终的阴影变换矩阵为：

$$
\begin{equation} \begin{aligned} \vec{M} &= \begin{bmatrix} 1 - \frac{N_x L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_x}{\vec{N} \cdot \vec{L}} & -\frac{d L_x}{\vec{N} \cdot {\vec{L}}} \ -\frac{N_x L_y}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_y L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_y}{\vec{N} \cdot \vec{L}} & -\frac{d L_y}{\vec{N} \cdot {\vec{L}}}\ -\frac{N_x L_z}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_z}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_z L_z}{\vec{N} \cdot \vec{L}} & -\frac{d L_z}{\vec{N} \cdot {\vec{L}}}\ 0 & 0 & 0 & 1 \ \end{bmatrix} \ &= \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} - \frac{1}{\vec{N} \cdot \vec{L}} \begin{bmatrix} N_x L_x & N_y L_x & N_z L_x & d L_x \ N_x L_y & N_y L_y & N_z L_y & d L_y \ N_x L_z & N_y L_z & N_z L_z & d * L_z\ 0 & 0 & 0 & 0 \ \end{bmatrix} \end{aligned} \end{equation}
$$

若向量采用行形式：

$$
\begin{equation} \begin{bmatrix} Q_x & Q_y & Q_z &1 \end{bmatrix} = \begin{bmatrix} P_x & P_y & P_z & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 - \frac{N_x L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_x L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_x L_z}{\vec{N} \cdot \vec{L}} & 0 \ -\frac{N_y L_x}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_y L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_z}{\vec{N} \cdot \vec{L}} & 0 \ -\frac{N_z L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_y}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_z L_z}{\vec{N} \cdot \vec{L}} & 0 \ -\frac{d L_x}{\vec{N} \cdot {\vec{L}}} & -\frac{d L_y}{\vec{N} \cdot {\vec{L}}} & -\frac{d L_z}{\vec{N} \cdot {\vec{L}}} & 1 \ \end{bmatrix} \end{equation}
$$

即：

$$
\begin{equation} \begin{aligned} \vec{M} &= \begin{bmatrix} 1 - \frac{N_x L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_x L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_x L_z}{\vec{N} \cdot \vec{L}} & 0 \ -\frac{N_y L_x}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_y L_y}{\vec{N} \cdot \vec{L}} & -\frac{N_y L_z}{\vec{N} \cdot \vec{L}} & 0 \ -\frac{N_z L_x}{\vec{N} \cdot \vec{L}} & -\frac{N_z L_y}{\vec{N} \cdot \vec{L}} & 1 - \frac{N_z L_z}{\vec{N} \cdot \vec{L}} & 0 \ -\frac{d L_x}{\vec{N} \cdot {\vec{L}}} & -\frac{d L_y}{\vec{N} \cdot {\vec{L}}} & -\frac{d L_z}{\vec{N} \cdot {\vec{L}}} & 1 \ \end{bmatrix} \ &= \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} - \frac{1}{\vec{N} \cdot \vec{L}} \begin{bmatrix} N_x L_x & N_x L_y & N_x L_z & 0 \ N_y L_x & N_y L_y & N_y L_z & 0 \ N_z L_x & N_z L_y & N_z L_z & 0 \ d L_x & d L_y & d * L_z & 0 \ \end{bmatrix} \end{aligned} \end{equation}
$$

UE实现

Shader

借助VF的计算接口获取顶点的WorldSpace，然后通过上述投影矩阵，将其投影到指定平面，再做透视投影

在此需要注意的是，VF计算出来的WorldSpace是经过预偏移的，需要减去偏移才能得到真正的投影矩阵：

#include "Common.ush"

#include "/Engine/Generated/Material.ush"
#include "/Engine/Generated/VertexFactory.ush"

float4x4 ProjectMatrix;

void MainVS( FVertexFactoryInput Input,
                #if MOBILE_MULTI_VIEW
                        , in uint ViewId : SV_ViewID
                #endif
                     out float4 OutPosition : SV_POSITION)
{
#if MOBILE_MULTI_VIEW
    const int MultiViewId = int(ViewId);
    ResolvedView = ResolveView(uint(MultiViewId));
#else
    ResolvedView = ResolveView();
#endif

    // ----------------------------------VertexFactory Require----------------------------------------------------
    FVertexFactoryIntermediates VFIntermediates = GetVertexFactoryIntermediates(Input);
    float4 WorldPositionExcludingWPO = VertexFactoryGetWorldPosition(Input, VFIntermediates);
    float4 WorldPosition = WorldPositionExcludingWPO;

    half3x3 TangentToLocal = VertexFactoryGetTangentToLocal(Input, VFIntermediates);        
    FMaterialVertexParameters VertexParameters = GetMaterialVertexParameters(Input, VFIntermediates, WorldPosition.xyz, TangentToLocal);

    WorldPosition.xyz += GetMaterialWorldPositionOffset(VertexParameters);
    // ----------------------------------------------------------------------------------------------------------

    // Project To Shadow Plane.
    WorldPosition.xyz -= ResolvedView.PreViewTranslation.xyz;
    WorldPosition = mul(WorldPosition, ProjectMatrix);
    WorldPosition.xyz += ResolvedView.PreViewTranslation.xyz;

    OutPosition = mul(WorldPosition, ResolvedView.TranslatedWorldToClip);
        
#if !OUTPUT_MOBILE_HDR && (COMPILER_GLSL_ES2 || COMPILER_GLSL_ES3_1 || COMPILER_GLSL_ES3_1_EXT)
    OutPosition.y *= -1;
#endif
}

float4 ShadowColor;

void MainPS(in  float4 svPos : SV_POSITION, 
                    out float4 outColor : SV_Target0)
{
    outColor = ShadowColor;
}

Shader C++ Implement

由于我们的shader是用于Mesh上的，因此shader需要继承自MeshMaterialShader

对于MeshMaterialShader，UE4有几个隐式限制：

必须绑定PassUniformBuffer
参数传递需通过FMeshMaterialShaderElementData的子类获取

在上述Shader中，VS需要参数：ProjectMaterix，PS需要参数：ShadowColor，需要定义如下结构：

class FPlaneShadowElementData : public FMeshMaterialShaderElementData
{
public:
    FMatrix ProjectMatrix;
    FLinearColor ShadowColor;
};

该shader并不需要每个材质都编译一份变种，我们新建一个DefaultPlaneShadowMaterial。仅在该材质上编译变种

static bool ShouldCompilePlaneShadowPermutation(const FMeshMaterialShaderPermutationParameters& Parameters)
{
    static const auto VarXGAllowPlaneShadow = IConsoleManager::Get().FindTConsoleVariableDataInt(TEXT("r.XGAllowPlaneShadow"));

    return IsMobilePlatform(Parameters.Platform)
            && UMaterial::IsDefaultPlaneShadowMaterial(Parameters.Material)
            && VarXGAllowPlaneShadow->GetValueOnAnyThread() != 0
            && Parameters.VertexFactoryType->IsUsedWithMaterials();
}

此时可以定义Shader对应的C++类：

template<int32 OutputFormat>
class FPlaneShadowVS : public FMeshMaterialShader
{
    DECLARE_SHADER_TYPE(FPlaneShadowVS, MeshMaterial)
public:
    FPlaneShadowVS() {}
    FPlaneShadowVS(const ShaderMetaType::CompiledShaderInitializerType& Initializer)
            : FMeshMaterialShader(Initializer)
    {
        ProjectMatrix.Bind(Initializer.ParameterMap, TEXT("ProjectMatrix"));
        PassUniformBuffer.Bind(Initializer.ParameterMap, TEXT("NotUsed"));
    }

    static bool ShouldCompilePermutation(const FMeshMaterialShaderPermutationParameters& Parameters)
    {
        return ShouldCompilePlaneShadowPermutation(Parameters);
    }

    static void ModifyCompilationEnvironment(const FMaterialShaderPermutationParameters& Parameters, FShaderCompilerEnvironment& OutEnvironment)
    {
        FMeshMaterialShader::ModifyCompilationEnvironment(Parameters, OutEnvironment);

        OutEnvironment.SetDefine(TEXT("OUTPUT_MOBILE_HDR"), OutputFormat == 1 ? 1 : 0);
    }

    virtual bool Serialize(FArchive& Ar) override
    {
        bool bShaderHasOutdatedParameters = FMeshMaterialShader::Serialize(Ar);
        Ar << ProjectMatrix;
        return bShaderHasOutdatedParameters;
    }

    void GetShaderBindings(
            const FScene* Scene,
            ERHIFeatureLevel::Type FeatureLevel,
            const FPrimitiveSceneProxy* PrimitiveSceneProxy,
            const FMaterialRenderProxy& MaterialRenderProxy,
            const FMaterial& Material,
            const FMeshPassProcessorRenderState& DrawRenderState,
            const FPlaneShadowElementData& ShaderElementData,
            FMeshDrawSingleShaderBindings& ShaderBindings) const
    {
            FMeshMaterialShader::GetShaderBindings(Scene, FeatureLevel, PrimitiveSceneProxy, MaterialRenderProxy, Material, DrawRenderState, ShaderElementData, ShaderBindings);
            ShaderBindings.Add(ProjectMatrix, ShaderElementData.ProjectMatrix);
    }

private:
    FShaderParameter ProjectMatrix;
};

class FPlaneShadowPS : public FMeshMaterialShader
{
    DECLARE_SHADER_TYPE(FPlaneShadowPS, MeshMaterial)

public:
    FPlaneShadowPS() {}
    
    FPlaneShadowPS(const ShaderMetaType::CompiledShaderInitializerType& Initializer)
            : FMeshMaterialShader(Initializer)
    {
        ShadowColor.Bind(Initializer.ParameterMap, TEXT("ShadowColor"));
        PassUniformBuffer.Bind(Initializer.ParameterMap, TEXT("NotUsed"));
    }

    static bool ShouldCompilePermutation(const FMeshMaterialShaderPermutationParameters& Parameters)
    {
        return ShouldCompilePlaneShadowPermutation(Parameters) && Parameters.PermutationId == 0;
    }

    static void ModifyCompilationEnvironment(const FMaterialShaderPermutationParameters& Parameters, FShaderCompilerEnvironment& OutEnvironment)
    {
        FMeshMaterialShader::ModifyCompilationEnvironment(Parameters, OutEnvironment);
    }

    virtual bool Serialize(FArchive& Ar) override
    {
        bool bShaderHasOutdatedParameters = FMeshMaterialShader::Serialize(Ar);
        Ar << ShadowColor;
        return bShaderHasOutdatedParameters;
    }

    void GetShaderBindings(const FScene* Scene,
                           ERHIFeatureLevel::Type FeatureLevel,
                           const FPrimitiveSceneProxy* PrimitiveSceneProxy,
                           const FMaterialRenderProxy& MaterialRenderProxy,
                           const FMaterial& Material,
                           const FMeshPassProcessorRenderState& DrawRenderState,
                           const FPlaneShadowElementData& ShaderElementData,
                           FMeshDrawSingleShaderBindings& ShaderBindings) const
    {
        FMeshMaterialShader::GetShaderBindings(Scene, FeatureLevel, PrimitiveSceneProxy, MaterialRenderProxy, Material, DrawRenderState, ShaderElementData, ShaderBindings);
    
        ShaderBindings.Add(ShadowColor, ShaderElementData.ShadowColor);
    }

private:
    FShaderParameter ShadowColor;
};

渲染管线修改

首先对于每个投影动态阴影的Mesh，都可能受多盏光源投射阴影。因此首先放弃类似于MobileBasePass的形式定义Processor，其依赖于MainView，会导致某些视野外但需要投射阴影的物体处理不到。因此，我们借助原有的ProjectedShadowInfo，每盏投影动态阴影的灯与每个角色都会产生一个ProjectedShadowInfo。

因此，只能动态构建MeshBatch，不能复用MainView的MeshBatch。通过动态新建MeshProcessor实现：

void FProjectedShadowInfo::SetMeshDrawCommandsForPlaneShadow(FSceneRenderer& Renderer)
{
    QUICK_SCOPE_CYCLE_COUNTER(STAT_SetupMeshDrawCommandsForPlaneShadow);

    FPlaneShadowPassMeshProcessor* MeshPassProcessor = new(FMemStack::Get()) FPlaneShadowPassMeshProcessor(Renderer.Scene,
                                                                                                           ShadowDepthView,
                                                                                                           ShadowDepthView->ViewUniformBuffer,
                                                                                                           nullptr,
                                                                                                           LightSceneInfo->Proxy->GetModulatedShadowColor(),
                                                                                                           GetGlobalShadowPlane(),
                                                                                                           LightSceneInfo->Proxy->GetDirection());

    if (Renderer.ShouldDumpMeshDrawCommandInstancingStats())
    {
        PlaneShadowPass.SetDumpInstancingStats(TEXT("PlaneShadow "));
    }

    const uint32 InstanceFactor = !GetShadowDepthType().bOnePassPointLightShadow || RHISupportsGeometryShaders(Renderer.Scene->GetShaderPlatform()) ? 1 : 6;

    PlaneShadowPass.DispatchPassSetup(Renderer.Scene,
                                      *ShadowDepthView,
                                      EMeshPass::Num,
                                      FExclusiveDepthStencil::DepthNop_StencilWrite,
                                      MeshPassProcessor,
                                      DynamicSubjectMeshElements,
                                      nullptr,
                                      NumDynamicSubjectMeshElements * InstanceFactor,
                                      SubjectMeshCommandBuildRequests,
                                      NumSubjectMeshCommandBuildRequestElements * InstanceFactor,
                                      PlaneShadowPassVisibleCommands);

    Renderer.DispatchedShadowDepthPasses.Add(&PlaneShadowPass);
}

FPlaneShadowPassMeshProcessor的定义如下:

class FPlaneShadowPassMeshProcessor : public FMeshPassProcessor
{
public:
    FPlaneShadowPassMeshProcessor(const FScene* Scene,
                                  const FSceneView* InViewIfDynamicMeshCommand,
                                  const TUniformBufferRef<FViewUniformShaderParameters>& InViewUniformBuffer,
                                  FMeshPassDrawListContext* InDrawListContext,
                                  const FLinearColor ShadowColor,
                                  const FPlane& ShadowPlane,
                                  const FVector& LightDir);

    virtual void AddMeshBatch(const FMeshBatch& RESTRICT MeshBatch, 
                              uint64 BatchElementMask, 
                              const FPrimitiveSceneProxy* RESTRICT PrimitiveSceneProxy, 
                              int32 StaticMeshId = -1) override final;

    FMeshPassProcessorRenderState PassDrawRenderState;

private:
    void Process(const FMeshBatch& RESTRICT MeshBatch,
                 uint64 BatchElementMask,
                 int32 StaticMeshId,
                 const FPrimitiveSceneProxy* RESTRICT PrimitiveSceneProxy,
                 const FMaterialRenderProxy* RESTRICT MaterialRenderProxy,
                 const FMaterial& RESTRICT MaterialResource,
                 ERasterizerFillMode MeshFillMode,
                 ERasterizerCullMode MeshCullMode);

    FLinearColor ShadowColor;
    FMatrix ProjectMatrix;
};

阴影的渲染方式采用Additive的形式，与之前ModulatedShadow的方案一致。减少场景的修改

1	PassDrawRenderState.SetBlendState(TStaticBlendState<CW_RGB, BO_Add, BF_Zero, BF_SourceColor, BO_Add, BF_Zero, BF_One>::GetRHI());

深度写入可以关闭，为了减少物体重叠造成的阴影加深，引入Stencil避免二次着色：

PassDrawRenderState.SetDepthStencilState(TStaticDepthStencilState<
                                         false, CF_DepthNearOrEqual, 
                                         true, CF_NotEqual, SO_Keep, SO_Keep, SO_Invert,
                                         false, CF_Never, SO_Keep, SO_Keep, SO_Keep,
                                         STENCIL_SANDBOX_MASK, STENCIL_SANDBOX_MASK>::GetRHI());
 PassDrawRenderState.SetStencilRef(0xff);

并在FPlaneShadowPassMeshProcessor的构造函数中计算好投影矩阵：

FMatrix CreatePlaneShadowProjectMatrix(const FVector LightDir, const FPlane& ShadowPlane)
{
#if UE_BUILD_DEVELOPMENT
    ensure(!FMath::IsNearlyZero(LightDir | ShadowPlane));
#endif
    float NDotL = LightDir | ShadowPlane;
    FVector Offset = -ShadowPlane.W / (LightDir | ShadowPlane) * LightDir;
    return FMatrix(FPlane(1 - ShadowPlane.X * LightDir.X / NDotL, 0 - ShadowPlane.X * LightDir.Y / NDotL, 0 - ShadowPlane.X * LightDir.Z / NDotL, 0),
                   FPlane(0 - ShadowPlane.Y * LightDir.X / NDotL, 1 - ShadowPlane.Y * LightDir.Y / NDotL, 0 - ShadowPlane.Y * LightDir.Z / NDotL, 0),
                   FPlane(0 - ShadowPlane.Z * LightDir.X / NDotL, 0 - ShadowPlane.Z * LightDir.Y / NDotL, 1 - ShadowPlane.Z * LightDir.Z / NDotL, 0),
                   FPlane(Offset.X, Offset.Y, Offset.Z, 1));
}

FPlaneShadowPassMeshProcessor::FPlaneShadowPassMeshProcessor(......)
{
    ......
    this->ShadowColor = ShadowColor;
    this->ProjectMaterial = CreatePlaneShadowProjectMatrix(LightDir, ShadowPlane);
}

AddMeshBatch负责计算MeshFillMode，MeshCullMode以及所使用的材质：这里直接使用默认材质

void FPlaneShadowPassMeshProcessor::AddMeshBatch(const FMeshBatch& RESTRICT MeshBatch, 
                                                 uint64 BatchElementMask, 
                                                 const FPrimitiveSceneProxy* RESTRICT PrimitiveSceneProxy, 
                                                 int32 StaticMeshId)
{
    if (MeshBatch.CastShadow)
    {
        const FMaterialRenderProxy& MaterialRenderProxy = *UMaterial::GetDefaultMaterial(MD_PlaneShadow)->GetRenderProxy();
        const FMaterial& Material = *MaterialRenderProxy.GetMaterial(FeatureLevel);

        const EBlendMode BlendMode   = Material.GetBlendMode();
        const bool bShouldCastShadow = Material.ShouldCastDynamicShadows();

        const ERasterizerFillMode MeshFillMode = ComputeMeshFillMode(MeshBatch, Material);
        ERasterizerCullMode FinalCullMode;
        {
            const ERasterizerCullMode MeshCullMode = ComputeMeshCullMode(MeshBatch, Material);

            const bool bTwoSided = Material.IsTwoSided() || PrimitiveSceneProxy->CastsShadowAsTwoSided();
            // Invert culling order when mobile HDR == false.
            static auto* MobileHDRCvar = IConsoleManager::Get().FindTConsoleVariableDataInt(TEXT("r.MobileHDR"));
            check(MobileHDRCvar);
            const bool bReverseCullMode = (RHINeedsToSwitchVerticalAxis(GShaderPlatformForFeatureLevel[FeatureLevel]) && MobileHDRCvar->GetValueOnAnyThread() == 0);
            FinalCullMode = bTwoSided ? CM_None : bReverseCullMode ? InverseCullMode(MeshCullMode) : MeshCullMode;
        }

        if (bShouldCastShadow
            && ShouldIncludeDomainInMeshPass(Material.GetMaterialDomain())
            && ShouldIncludeMaterialInDefaultOpaquePass(Material))
        {
            Process(MeshBatch, BatchElementMask, StaticMeshId, PrimitiveSceneProxy, &MaterialRenderProxy, Material, MeshFillMode, FinalCullMode);
        }
    }
}

在Process中最终构建出MeshDrawCommand，用于后续渲染:

void FPlaneShadowPassMeshProcessor::Process(const FMeshBatch& RESTRICT MeshBatch, 
                                            uint64 BatchElementMask, 
                                            int32 StaticMeshId, 
                                            const FPrimitiveSceneProxy* RESTRICT PrimitiveSceneProxy, 
                                            const FMaterialRenderProxy* RESTRICT MaterialRenderProxy, 
                                            const FMaterial& RESTRICT MaterialResource, 
                                            ERasterizerFillMode MeshFillMode, 
                                            ERasterizerCullMode MeshCullMode)
{
    const FVertexFactory* VertexFactory = MeshBatch.VertexFactory;
    
    FPlaneShadowElementData ElementData;
    ElementData.InitializeMeshMaterialData(ViewIfDynamicMeshCommand, PrimitiveSceneProxy, MeshBatch, StaticMeshId, false);
    ElementData.ShadowColor   = ShadowColor;
    ElementData.ProjectMatrix = ProjectMatrix;

#define SELECT_PLANESHADOW_SHADER(shaderType)\
{\
	TMeshProcessorShaders<shaderType, FBaseHS, FBaseDS, FPlaneShadowPS> PlaneShadowPassShaders;\
    \
    PlaneShadowPassShaders.VertexShader = MaterialResource.GetShader<shaderType>(VertexFactory->GetType());\
    PlaneShadowPassShaders.PixelShader = MaterialResource.GetShader<FPlaneShadowPS>(VertexFactory->GetType());\
    \
    const FMeshDrawCommandSortKey SortKey = CalculateMeshStaticSortKey(PlaneShadowPassShaders.VertexShader, PlaneShadowPassShaders.PixelShader);\
    \
    BuildMeshDrawCommands(MeshBatch,\
                BatchElementMask,\
                PrimitiveSceneProxy,\
                *MaterialRenderProxy,\
                MaterialResource,\
                PassDrawRenderState,\
                PlaneShadowPassShaders,\
                MeshFillMode,\
                MeshCullMode,\
                SortKey,\
                EMeshPassFeatures::Default,\
                ElementData);\
    }

    if (IsMobileHDR())
        SELECT_PLANESHADOW_SHADER(FPlaneShadowVS_HDR)
    else
        SELECT_PLANESHADOW_SHADER(FPlaneShadowVS_LDR)
        
#undef SELECT_PLANESHADOW_SHADER

}

Capsule Shadow

Contact Shadow

Virtual Shadow Map

Ref

https://learnopengl.com/Advanced-Lighting/Shadows/Shadow-Mapping

https://zhuanlan.zhihu.com/p/370951892

https://www.cnblogs.com/KillerAery/p/15201310.html#percentage-closer-filteringpcf

https://microsoft.github.io/DirectX-Specs/d3d/archive/D3D11_3_FunctionalSpec.htm#inst_GATHER4

https://www.flyandnotdown.com/post/3f3b31e8-f589-4e02-9b28-2c3c19f6f79b

Shadow

基本实现

Bias

Depth Bias

Slope Scale Depth Bias

Normal Bias

Caster Bias & Receiver Bias

PCF

连续Tent Filter

PCSS

CSM

投影半径

Bias

隔帧更新

Scrolling

Variance Shadow Map

RSM

ShadowVolume

PlaneShadow

公式推导

UE实现

Shader

Shader C++ Implement

渲染管线修改

Capsule Shadow

Contact Shadow

Virtual Shadow Map

Ref

Comments

Your browser is out-of-date!