Contents
Snell’s Law
$$ \begin{align} \eta{_1} \sin(\theta_1) &\quad = \eta{_2}\sin(\theta{_2}) & n &\quad = (0,1) \notag \\\\[2ex] L\qquad &\quad = (-\sin(\theta_1) , \cos(\theta_1)) & T &\quad = (\sin(\theta_2) , -\cos(\theta_2))\notag \end{align} $$设:
$$\overrightarrow{T} = x \times \overrightarrow{L} + y \times \overrightarrow{n} $$ $$ \begin{align} \Rightarrow & \begin{cases} &\sin(\theta_2) &= &\quad -\sin(\theta_1) \times x + 0 \times y \notag \\\\[2ex] &-\cos(\theta_2) &= &\quad \cos(\theta_1) \times x + 1 \times y \notag \end{cases} \\\\[2ex] \Rightarrow & \begin{cases} x &= -\frac{\sin(\theta_2)}{\sin(\theta_1)} \notag \\\\[2ex] y &= \cos(\theta_1) * \frac{\sin(\theta_2)}{\sin(\theta_1)} - \cos(\theta_2) \notag \end{cases} \end{align} $$ $$ \begin{align} \Rightarrow \overrightarrow{T} &= -\frac{\sin(\theta_2)}{\sin(\theta_1)} \times \overrightarrow{L} + (\cos(\theta_1) \times \frac{\sin(\theta_2)}{\sin(\theta_1)} - \cos(\theta_2)) \times \overrightarrow{n} \notag \\\\[2ex] \because \cos(\theta_2) &= \sqrt{1 - \sin^2(\theta_2)} \notag \\\\ &= \sqrt{1 - \frac{\sin^2(\theta_2)}{\sin^2(\theta_1)}(1 - \cos^2(\theta_1))} \notag \\\\ &= \sqrt{1 - \frac{\sin^2(\theta_2)}{\sin^2(\theta_1)}(1 - (\overrightarrow{L} \cdot \overrightarrow{n})^2)}\notag \end{align} $$ $$ \begin{align} \Rightarrow \overrightarrow{T} &= -\frac{\sin(\theta_2)}{\sin(\theta_1)} \times \overrightarrow{L} + (\cos(\theta_1) \times \frac{\sin(\theta_2)}{\sin(\theta_1)} - \sqrt{1 - \frac{\sin^2(\theta_2)}{\sin^2(\theta_1)}(1 - (\overrightarrow{L} \cdot \overrightarrow{n})^2)}) \times \overrightarrow{n}\notag \\\\[2ex] &= -\frac{\eta_1}{\eta_2} \times \overrightarrow{L} + \overrightarrow{n}(\frac{\eta_1}{\eta_2}(\overrightarrow{L} \cdot \overrightarrow{n}) - \sqrt{1 - \frac{\eta_1^2}{\eta_2^2}(1 - (\overrightarrow{L} \cdot \overrightarrow{n})^2)})\notag \end{align} $$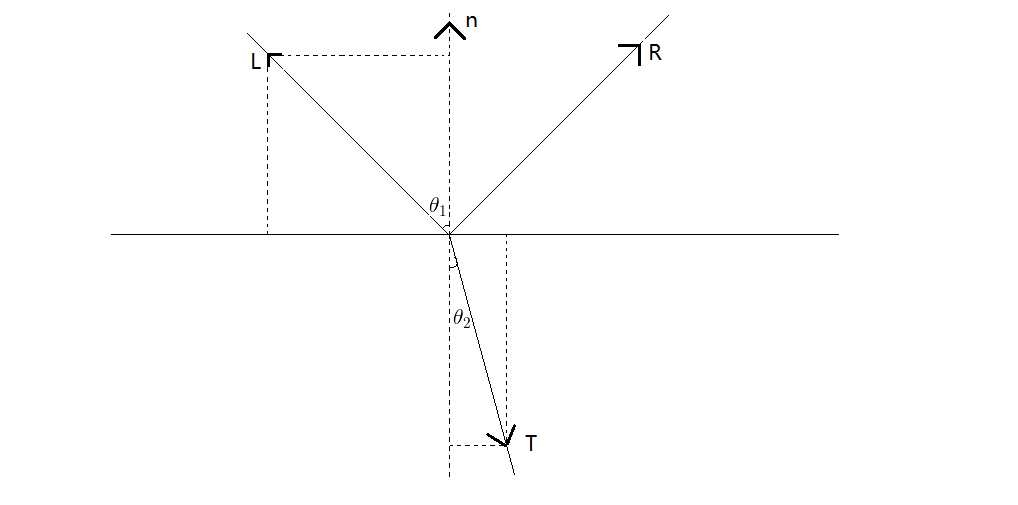
Comments